Halo adik-adik ajar hitung.. kembali lagi dengan postingan terbaru dari ajar hitung. Hari ini kita akan latihan soal tentang integral. Yuk semangat.. kita mulai ya..
Kalian bisa pelajari materi ini melalui channel YouTube ajar hitung. Silahkan klik link video berikut:
a. ½ x4 – x3 + 7x + C
b. ½ x4 + x3 + 7x + C
c. ½ x4 + x3 - 7x + C
d. ½ x4 – x3 - 7x + C
e. 1/3 x4 + x3 - 7x + C
Jawab:
= ½ x4 + x3 – 7x + C
Jawaban yang tepat C.
a. 2(5x3 – 12)8 + C
b. (5x3 – 12)8 + C
c. ½ (5x3 – 12)8 + C
d. ¼ (5x3 – 12)8 + C
e. 1/8 (5x3 – 12)8 + C
Jawab:
Misal u = 5x3 – 12
du/dx = 15x2
du = 15x2 . dx
dx = du/15x2
Jawaban yang tepat E.
a. 3x√x + 2√x + 6x + C
b. 3x√x + √x + 6x + C
c. 2x√x + 2√x + 6x + C
d. 2/3x√x + 2√x + 6x + C
e. 3/4x√x + 2√x + 6x + C
Jawab:
= 2x√x + 2√x + 6x + C
Jawaban yang tepat C.
4. Jika F(x) =  dx, dan F(0) = 5, maka F(x) sama dengan ...
dx, dan F(0) = 5, maka F(x) sama dengan ...
a. x3 + x2 + 2x + 7
b. x3 + x2 + 2x + 6
c. x3 + x2 + 2x + 5
d. x3 + x2 + 2x + 4
e. x3 + x2 + 2x + 3
Jawab:
= x3 + x2 + 2x + C
F(0) = 5
x3 + x2 + 2x + C = 5
0)3 + (0)2 + 2(0) + C = 5
C = 5
Maka F(x) = x3 + x2 + 2x + 5
Jawaban yang tepat C.
5. Gradien sebuah garis singgung kurva di titik (x , y) adalah 2x – 7. Jika kurva tersebut melalui titik (4, -2), maka persamaan kurva tersebut adalah...
a. y = x2 + 7x + 10
b. y = x2 - 7x - 10
c. y = 2x2 - 7x + 10
d. y = x2 - 7x + 10
e. y = 3x2 - 7x + 10
Jawab:
dxKurva melalui titik (4, -2), maka subtitusikan x = 4 dan y = -2
y = x2 – 7x + C
-2 = (4)2 – 7(4) + C
-2 = 16 – 28 + C
-2 = -12 + C
C = -2 + 12
C = 10
Maka, persamaan kurvanya menjadi: y = x2 – 7x + 10
Jawaban yang tepat D.
6. Sebuah partikel bergerak dengan kecepatan v(t) = 3t2 + 6t – 4. Jika pada saat t = 1 posisi partikel berada pada jarak 4 m, maka persamaan lintasan partikel tersebut adalah...
a. s(t) = t3 + 3t2 – 4t + 1
b. s(t) = 2t3 + 3t2 – 4t + 4
c. s(t) = t3 + 3t2 – 4t + 4
d. s(t) = 1/3 t3 + 3t2 – 2t + 4
e. s(t) = t3 + 2t2 – 4t + 4
Jawab:
= t3 + 3t2 – 4x + C
pada saat t = 1 posisi partikel berada pada jarak 4 m, maka subtitusikan t = 1 dan S = 4
S(t) = t3 + 3t2 – 4x + C
4 = (1)3 + 3(1)2 – 4(1) + C
4 = 1 + 3 – 4 + C
4 = 0 + C
C = 4
Maka persamaan lintasannya menjadi S(t) = t3 + 3t2 – 4x + 4
Jawaban yang tepat C.
7. Sebuah mobil bergerak sepanjang lintasan dengan persamaan percepatan a(t) = 3t2 – 18t + 24. Jika kecepatan benda pada saat 2 detik adalah 70 m/s, maka persamaan kecepatan mobil tersebut adalah...
a. v(t) = 3t3 – 18t2 + 24t + 50
b. v(t) = t3 – 9t2 + 24t + 50
c. v(t) = t3 – 18t2 + 24t - 50
d. v(t) = 3t3 – 9t2 + 24t + 50
e. v(t) = 2t3 – 9t2 + 24t + 50
Jawab:
= t3 – 9t2 + 24t + C
kecepatan benda pada saat 2 detik adalah 70 m/s, maka subtitusikan t = 2 dan v = 70
V(t) = t3 – 9t2 + 24t + C
70 = (2)3 – 9(2)2 + 24(2) + C
70 = 8 – 36 + 48 + C
70 = 20 + C
C = 70 – 20
C = 50
Maka persamaan kecepatannya menjadi: V(t) = t3 – 9t2 + 24t + 50
Jawaban yang tepat B.
Jawab:
= (2/3 . 8 + 2) – (2/3 (-1) – 1)
= (16/3 + 2) – (-2/3 – 3/3)
= (16/3 + 6/3) + 5/3
= 22/3 + 5/3
= 27/3
= 9
Jawaban yang tepat E.
a. 9 1/3
b. 9
c. 8
d. 10/3
e. 3
Jawab:
= (1/3 . 27 + ½ ) – (1/3 + 1/6)
= (9 + ½ ) – (2/6 + 1/6)
= 19/2 – 3/6
= 19/2 – ½
= 18/2
= 9
Jawaban yang tepat B.
a. 4
b. 5
c. 6
d. 7
e. 8
Jawab:
= (2(2)3 – 4(2)2 + 4(2)) – (2(1)3 – 4(1)2 + 4(1))
= (2.8 – 4.4 + 8) – (2 – 4 + 4)
= (16 – 16 + 8) – 2
= 8 – 2
= 6
Jawaban yang tepat C.
Jawab:
= (1/3 . 27 + 3) – (1/3 + 1)
= (9 + 3) – (1/3 + 3/3)
= 12 – 4/3
= 36/3 – 4/3
= 32/3
= 10 2/3
Jawaban yang tepat A.
12. Jika f(x) = ax + b,  dx = 1, dan
dx = 1, dan  dx = 5, maka nilai a + b adalah...
dx = 5, maka nilai a + b adalah...
a. 3
b. 4
c. 5
d. -3
e. -4
Jawab:
(a/2 (1)2 + b(1)) – (a/2 (0)2 + b(0)) = 1
(a/2 + b) – 0 = 1
a/2 + b = 1 (kalikan 2)
a + 2b = 2 .... (persamaan i)
(a/2 (2)2 + b(2)) – (a/2 (1)2 + b(1)) = 5
(a/2 (4) + 2b) – (a/2 + b) = 5
(2a + 2b) – (a/2 + b) = 5
2a – a/2 + 2b – b = 5
4a/2 – a/2 + b = 5
3a/2 + b = 5 (kalikan dengan 2)
3a + 2b = 10 .... (persamaan ii)
Eliminasikan persamaan (i) dengan persamaan (ii):
2a = 8
a = 8/2
a = 4
Subtitusikan a = 4 untuk mencari b:
a + 2b = 2
4 + 2b = 2
2b = 2 – 4
2b = -2
b = -2/2
b = -1
Maka nilai a + b = 4 + (-1) = 3
Jawaban yang tepat A.
a. -1
b. – ½
c. 0
d. 1
e. 2
Jawab:
= (- ½ cos (2 (π/2) - π) - (- ½ cos (2 (0) - π)
= (- ½ cos π - π) – (- ½ cos - π)
= (- ½ cos 0) – 0
= - ½ (1) – 0
= - ½
Jawaban yang tepat B.
a. ¼ (π2 + 3π)
b. 2/3 (π2 + 3π)
c. 1/3 (π2 + 3π)
d. ½ (π2 + 3π) + 1
e. 2/3 (π2 + 3π) + 1
Jawab:
= (2 (π/2)2 + 3(π/2) + sin π/2![]() ) - (2 (0)2 + 3(0) + sin 0 )
) - (2 (0)2 + 3(0) + sin 0 )
= (2 . π2/4 + 3π/2 + sin 900) – 0
= π2/2 + 3π/2 + 1
= ½ (π2 + 3 π) + 1
Jawaban yang tepat D.
a. – ¼
b. – ½
c. 0
d. -1
e. 2
Jawab:
= ( - ½ cos 2(π)) – ( - ½ cos 2(0))
= (- ½ . 1) – 0
= - ½
Jawaban yang tepat B.
Jawab:
= - ½ x-2 – 3x + C
Jawaban yang tepat B.
Jawab:
Misal u = x3 + 8
du/dx = 3x2
du = 3x2 . dx
dx = du/3x2
Jawaban yang tepat D.
a. 3 sin x – x3 + tx + C
b. 3 sin x – 2/3 x3 + tx + C
c. 3 cos x – 2/3 x3 + tx + C
d. 3 cos x – 2/3 x3 + x + C
e. 3 cos x – x3 + tx + C
Jawab:
= 3 sin x – 2/3 x3 + tx + C
Jawaban yang tepat B.
19. Luas daerah yang dibatasi kurva y = 6x, sumbu X, dan garis x = 5 adalah...
a. 25 satuan luas
b. 75 satuan luas
c. 100 satuan luas
d. 225 satuan luas
e. 625 satuan luas
Jawab:
= (3 (5)2) – 3 (0)2
= 75 – 0
= 75
Jadi jawaban yang tepat B.
20. Luas daerah yang diarsir pada gambar di bawah ini adalah...
a. 3 satuan luas
b. 4 satuan luas
c. 5 satuan luas
d. 6 satuan luas
e. 7 satuan luas
Jawab:
= (1/3 (2)3 + 2) – (1/3 (-1)3 + (-1)
= (8/3 + 2) – (-1/3 – 1)
= (8/3 + 6/3) – (-1/3 – 3/3)
= 14/3 + 4/3
= 18/3
= 6
Jawaban yang tepat D.
21. Volume benda putar yang terjadi jika daerah pada kuadran pertama yang dibatasi oleh kurva x = y2 – 1, sumbu x, sumbu Y, diputar mengelilingi sumbu Y adalah....
a. 52/15 π satuan volume
b. 16/12 π satuan volume
c. 16/15 π satuan volume
d. π satuan volume
e. 12/15 π satuan volume
Jawab:
- Titik potong kurva dengan sumbu Y =
x = y2 – 1
0 = y2 – 1
0 = (y + 1)(y – 1)
y + 1 = 0 maka y = -1
dan
y – 1 = 0 maka y = 1
V = π(1/5 (1)5 – 2/3 (1)3 + 1)
- (1/5 (-1)5 – 2/3 (-1)3 + (-1))
V = π(1/5 – 2/3 + 1) – (-1/5 + 2/3 – 1)
V = π (8/15 – (-8/15)
V = 16/15 π
Jawaban yang tepat C.
22. Volume benda putar yang terjadi jika daerah antara y = 1/3 x dan y2 = x diputar mengelilingi sumbu Y sejauh 3600 adalah...
a. 52 2/5 π satuan volume
b. 32 2/3 π satuan volume
c. 32 2/5 π satuan volume
d. 22 2/5 π satuan volume
e. 4 1/2 π satuan volume
Jawab:
y = 1/3 x
x = 3y
dan
x = y2
Titik potong garis dan kurva di atas terhadap sumbu Y adalah:
x = x
3y = y2
y2 – 3y = 0
y(y – 3) = 0
y = 0
dan
y – 3 = 0
y = 3
V = π(1/5 (3)5 – 3(3)3) – (1/5 (0)5 – 3(0)3)
V = π (243/5 – 81/5)
V = π 162/5
V = 32 2/5 π
Jawaban yang tepat C.
23. Volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 3x – 2, garis x = 1, dan garis x = 3 diputar mengelilingi sumbu X adalah.... satuan volume.
a. 34 π
b. 38 π
c. 46 π
d. 48 π
e. 50 π
Jawab:
V = π (3(3)3 – 6(3)2 + 4(3)) – (3(1)3 – 6(1)2 + 4(1))
V = π (81 – 54 + 12) – (3 – 6 + 4)
V = π (39 – 1)
V = 38 π
Jawaban yang tepat B.
24. Volume benda putar yang terjadi jika kurva y = 16 – x2 diputar mengelilingi sumbu y sejauh 3600 adalah...
a. 128 π satuan volume
b. 36 π satuan volume
c. 24 π satuan volume
d. 18 π satuan volume
e. π satuan volume
Jawab:
y = 16 – x2 (kita ubah ke dalam bentuk x sama dengan)
x2 = 16 – y
Titik potong kurva dengan sumbu Y:
y = 16 – x2
0 = (4 – x)(4 + x)
4 – x = 0
x = 4
dan
4 + x = 0
x = -4
V = π (16(4) – ½ (4)2) – (16(-4) – ½ (-4)2)
V = π (64 – 8) – (-64 – 8)
V = π (56 + 72)
V = 128 π
Jawaban yang tepat A.
25. Daerah yang dibatasi oleh kurva y = x2 dan garis x + y – 2 = 0 diputar mengelilingi sumbu x sejauh 3600. Volume benda putar yang terjadi adalah...
a. 15 2/3 π satuan volume
b. 15 2/5 π satuan volume
c. 14 3/5 π satuan volume
d. 14 2/5 π satuan volume
e. 10 3/5 π satuan volume
Jawab:
Titik potong kurva dan garis dengan sumbu X:
kurva y = x2 dan
garis x + y – 2 = 0 atau y = 2 – x
x2 = 2 – x
x2 + x – 2 = 0
(x – 1)(x + 2) = 0
x – 1 = 0
x = 1
dan
x + 2 = 0
x = -2
V = π (1/3 – 2 + 4 – 1/5) – (-8/3 – 8 – 8 + 32/5)
V = π (5/15 + 2 – 3/15) – (-40/15 + 96/15 – 16)
V = π (2/15 + 30/15) – (56/15 – 240/15)
V = π (32/15 + 184/15)
V = 216/15 π
V = 14 6/15 π
V = 14 2/5 π
Jawaban yang tepat D.
26. Daerah D dibatasi oleh y = sin x, 0 ≤ x ≤ π dan sumbu X. Jika daerah D diputar terhadap sumbu X, maka volume benda putar yang terjadi adalah...
a. π satuan volume
b. π2 satuan volume
c. ½ π2 satuan volume
d. 2 π satuan volume
e. 2π2 satuan volume
Jawab:
V = π (1/2 π – 0) – 0
V = ½ π2
Jawaban yang tepat C.
Sampai disini ya adik-adik latihan soal kita hari ini. Sampai bertemu di latihan soal yang selanjutnya...







































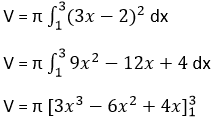



No comments:
Post a Comment