Halo adik-adik.. postingan ini adalah postingan lanjutan dari postingan sebelumnya. Jadi, postingan ini akan kakak mulai dari nomor 21. Bagi kalian yang ketinggalan nomor 1 – 20 bisa cek dengan cara klik link DISINI. Yuk kita mulai...
Kalian sudah bisa mempelajari latihan soal ini melalui akun youtube ajar hitung. Untuk mudahnya, kalian bisa langsung klik video link di bawah ini ya..
a. -90
b. -60
c. -30
d. 60
Jawab:
Jawaban yang tepat B.
22. Persamaan sumbu simetri dari fungsi kuadrat f(x) = x2 + 2x – 3 adalah...
a. x = -2
b. x = -1
c. x = 0
d. x = 1
Jawab:
f(x) = x2 + 2x – 3 memiliki a = 1; b = 2; dan c = -3
Rumus mencari sumbu simetri =
Jawaban yang tepat adalah B.
23. Diketahui fungsi kuadrat y = -x2 + 2x + 3. Grafik fungsi kuadrat tersebut adalah...
Jawab:
Langkah pertama, cari titik potong sumbu x (y = 0)
-x2 + 2x + 3 = 0
(-x + 3) (x + 1) = 0
-x + 3 = 0 dan x + 1 = 0
x = 3 x = -1
Jadi titik potong sumbu X = (-1, 0) dan (3, 0)
Dari sini kita sudah dapat melihat, bahwa jawaban yang tepat adalah A.
24. Persamaan sumbu simetri dan fungsi kuadrat y = x2 – 6x + 9 adalah..
a. x = 1
b. x = 2
c. x = 3
d. x = 4
Jawab:
x2 – 6x + 9 memiliki a = 1; b = -6 dan c = 9
Persamaan sumbu simetri =
Jawaban yang tepat C.
25. Fungsi kuadrat yang mempunyai persamaan sumbu simetri x = - ¼ adalah ...
a. y = 2x2 + x – 10
b. y = -2x2 - x + 10
c. y = 2x2 - x + 10
d. y = -2x2 + x + 10
Jawab:
Kita cari satu persatu sumbu simetri dari pilihan di atas:
Jawaban yang tepat adalah A dan B.
26. Persamaan fungsi grafik yang memotong sumbu X di titik R(1, 0) dan T(5, 0), serta melalui titik (2,3) adalah...
a. y = x2 + 3x + 5
b. y = 2x2 + 3x - 5
c. y = -x2 + 6x - 5
d. y = x2 + 6x + 5
Jawab:
Rumusnya : y = a(x – x1)(x – x2)
R(1, 0) dan T(5, 0) maka x1 = 1 dan x2 = 5
Melalui titik (2, 3) maka x = 2 dan y = 3
y = a(x – x1)(x – x2)
3 = a(2 – 1)(2 – 5)
3 = a(1)(-3)
3 = -3a
a = -3 : 3
a = -1
Maka persamaan garisnya adalah =
y = (-1)(x – 1)(x – 5)
y = -1(x2 -5x – x + 5)
y = -1(x2 -6x + 5)
y = -x2 + 6x – 5
Jawaban yang tepat adalah C.
27. Persamaan fungsi kuadrat yang grafiknya melalui A(0, -6); B(-1, 0); dan C(1, -10) adalah...
a. y = x2 - 2x – 8
b. y = x2 + 2x – 8
c. y = x2 - 5x – 6
d. y = x2 - 5x + 6
Jawab:
y = ax2 + bx + c
Titik A(0, -6) maka: -6 = a(0)2 + b(0) + c
-6 = c ..... (persamaan i)
Titik B(-1, 0) maka: 0 = a(-1)2 + b(-1) + c
0 = a – b + c
0 = a – b + (-6) (Subtitusikan c = -6 pada persamaan di atas)
0 = a – b – 6
-a + b = -6 ..... (persamaan ii)
Titik C(1, -10) maka: 10 = a(1)2 + b(1) + c
-10 = a + b + c (subtitusi c = -6)
-10 = a + b – 6
a + b = -10 + 6
a + b = -4 ..... (persamaan iii)
Eliminasikan persamaan ii dan iii:
subtitusikan a = 1 pada persamaan a + b = -4
1 + b = -4
b = -4 – 1
b = -5
Maka ditemukan a = 1; b = -5; dan c = -6. Maka persamaan fungsi kuadratnya =
y = ax2 + bx + c
y = (1)x2 + (-5)x + (-6)
y = x2 – 5x – 6
Jawaban yang tepat adalah C.
28. Titik puncak dari fungsi grafik y = x2 – 2x – 3 adalah...
a. (0, 4)
b. (4, 0)
c. (1, -4)
d. (4, 1)
Jawab:
y = x2 – 2x – 3 memiliki a = 1; b = -2; c = -3
Titik puncaknya:
Subtitusikan x = 1 pada persamaan y = x2 – 2x – 3 untuk mencari titik Y
y = x2 – 2x – 3
y = (1)2 – 2(1) – 3
y = 1 – 2 – 3
y = -4
Jadi titik puncaknya = (1, -4)
Jawaban yang tepat C.
29. Perhatikan grafik fungsi kuadrat berikut!
Persamaan fungsi kuadratnya adalah..
Jawab:
Pada gambar diketahui titik puncak (2, 9) memiliki xp = 2 dan yp =9
Salah satu titik (5, 0) memiliki x = 5 dan y = 0
Kita pakai rumus: y = a(x – xp)2 + yp
0 = a(5 – 2)2 + 9
0 = a(3)2
+ 9
0 = 9a + 9
9a = -9
a = -9 : 9
a = -1
Maka persamaan grafik di atas adalah:
y = a(x – xp)2
+ yp
y = -1(x – 2)2
+ 9
y = -1(x2 –
4x + 4) + 9
y = -x2 + 4x
– 4 + 9
y = -x2 + 4x
+ 5
Jawaban yang tepat C.
30. Akar-akar persamaan kuadrat x2 – 6x – 2 = 0 adalah...
Jawab:
Dari Pilihan gandanya terlihat kita harus menggunakan rumus abc.
x2 – 6x – 2 = 0 memiliki a = 1; b = -6; dan c = -2
Jawaban yang tepat B.
a. 2√2 - √2
b. 2√2 + √2
c. √7 - √3
d. √6 - 2
Jawab:
Jawaban yang tepat D.
32. Bentuk sederhana dari  adalah ...
adalah ...
a. 3/2(√2 - 2)
b. 3/2√2 - 2
c. 3/2(√2 - 4)
d. 3/2√2 - 4
Jawab:
Jawaban yang tepat B.
33. Grafik yang tepat untuk fungsi kuadrat y = x2 – 6x + 9 adalah...
Jawab:
x2 – 6x + 9 memiliki a = 1; b = -6; dan c = 9
Kita cari sumbu simetrinya:
Subtitusikan x = 3 ke persamaan y = x2 – 6x + 9
y = (3)2 –
6(3) + 9
y = 9 – 18 + 9
y = -9 + 9
y = 0
Maka titik puncaknya (3, 0)
Pada pilihan ganda hanya A dan C yang memiliki titik puncak (3, 0). y = x2 – 6x + 9 memiliki nilai a > 0, maka parabola seharusnya terbuka ke atas.
Jawaban yang tepat adalah C.
34. Persamaan kuadrat yang akar-akarnya 5 dan -2 adalah ...
a. x2 + 3x – 10 = 0
b. x2 - 3x – 10 = 0
c. x2 + 3x + 10 = 0
d. x2 + 7x + 10 = 0
Jawab:
Kita cari satu persatu akar-akar dari pilihan di atas.
(x + 5)(x – 2) = 0
x + 5 = 0 dan x – 2 = 0
x = -5 x = 2
(x - 5)(x + 2) = 0
x – 5 = 0 dan x + 2 = 0
x = 5 x = -2
Jawaban yang tepat B.
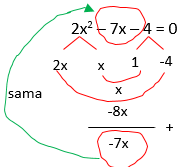
35. Diketahui fungsi kuadrat f(x) = 2x2 – 7x – 4. Titik potong grafik fungsi kuadrat tersebut dengan sumbu X dan sumbu Y berturut-turut adalah...
a. (-1, 0), (2, 0), dan (0, -4)
b. (-1, 0), (1/2 , 0), dan (4, 0)
c. (-1/2, 0), (4, 0), dan (0, -4)
d. (4, 0), (2, 0), dan (-1, 0)
Jawab:
a. Titik potong sumbu x (y = 0)
y = 2x2 – 7x
– 4
(2x + 1)(x – 4) = 0
2x + 1 = 0 dan x – 4 = 0
2x = -1 x = 4
x = -1/2
Jadi, titik potong dengan sumbu X = (-1/2, 0) dan (4, 0)
b. Titik potong sumbu Y (x = 0)
y
= 2x2 – 7x – 4
y
= 2(0)2 – 7(0) – 4
y = 0 – 0 – 4
y = -4
Jadi, titik potong dengan sumbu Y = (0, -4)
Jawaban yang tepat C.
36. Bayangan titik P(3, -4) oleh dilatasi (0, k) adalah P’(15, -20) sehingga bayangan titik Q(-5, -7) oleh (0, 2k) adalah...
a. (10, 14)
b. (20, 35)
c. (-35, 42)
d. (-50, -70)
Jawab:
Rumus dilatasi dengan pusat (0, 0) dan faktor dilatasi k.
Maka:
kx = 15
k(3) = 15
k = 15 : 3
k = 5
Nilai k = 5
Nilai 2k = 2(5) = 10
Bayangan Q(-5, -7) adalah:
Jawaban yang tepat D.
37 Titik A dengan koordinat di (3, 2) dan B dengan koordinat di (1, -2). Bayangan titik A dan B setelah direfleksikan oleh sumbu Y adalah ...
a. A’(2, 3) dan B’(-2, 1)
b. A’(-2, 2) dan B’(2, 3)
c. A’(-3, 2) dan B’(-1, -2)
d. A’(1, 2) dan B’(3, 2)
Jawab:
Rumus refleksi terhadap sumbu Y:
Hasil refleksi titik A:
Hasil refleksi titik B;
Jawaban yang tepat C.
38. Titik P berkoordinat (1, 2) dan titik Q berkoordinat (3, 1), ditranslasikan lima satuan ke kiri dan tiga satuan ke bawah, maka P’ dan Q’ berturut-turut adalah...
a. (-4, -1) dan (-2, -2)
b. (-2, -2) dan (-4, -1)
c. (4, -1) dan (-2, -2)
d. (4, -1) dan (-1, -4)
Jawab:
Rumus bayangan translasi:
Bayangan titik P:
Bayangan titik Q:
Jawaban yang tepat A.
39. Titik M(5, 2) dan N(-5, -3) dirotasikan 900 dengan pusat rotasi 0(0, 0) maka nilai M’ dan N’ adalah...
a. (-2, 5) dan (3, -5)
b. (-5, -2) dan (5, 3)
c. (5, -2) dan (5, 3)
d. (-5, 2) dan (-5, -3)
Jawab:
Rumus rotasi 900 adalah:
Bayangan titik M:
Bayangan titik N:
Jawaban yang tepat A.
40. Segitiga ABC berkoordinat di A(7, 10); B(4, -6); dan C(-2, 3), maka bayangan segitiga ABC setelah didilatasi yang berpusat di titik asal dengan faktor skala 2 adalah...
a. A’(-4, 6); B’(8, 12); dan C’(14, 20)
b. A’(14, 20); B’(8, -12); dan C’(-4, 6)
c. A’(8, -12); B’(14, 20); dan C’(-4, 6)
d. A’(-4, 6); B’(14, 20); dan C’(8, -12)
Jawab:
Rumus dilatasi dengan pusat (0, 0) dan faktor dilatasi k.
Bayangan titik A:
Bayangan titik B:
Bayangan titik C:
Jawaban yang tepat B.
Selamat mempersiapkan diri untuk UAS ya adik-adik.. semoga kalian mendapatkan nilai seperti yang kalian harapkan...













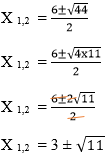
























TERIMA KASIH KAK SEMOGA BERKAH ILMUNYA, MUDAH REZEKINYA
ReplyDeleteAmiiin.... semoga artikelnya dapat membantu...
Delete