Hai adik-adik... tidak terasa kita sudah sampai di pertengahan semester 2. Itu tandanya PTS sebentar lagi. Yuk persiapkan diri kalian dari sekarang. Mari kakak temani...
1. Jika titik A (2, -7) ditranslasikan oleh T = bayangannya adalah...
bayangannya adalah...
a. A’(2, -3)
b. A’(5, -5)
c. A’(4, 3)
d. A’(-4, -2)
Jawab:
Rumus translasi titik A(x, y) oleh translasi T = (a b) adalah:
Pada soal diketahui A(2, -7) dan T =  maka:
maka:
Jadi bayangannya adalah A’(5, -5)
Jawaban yang tepat B.
2. Bayangan titik P(-3, 5) jika dicerminkan terhadap garis y = -x adalah...
a. (-5, 3)
b. (-3, -5)
c. (2, 5)
d. (-5, -2)
Jawab:
Rumus bayangan titik P(x, y) oleh pencerminan garis y = -x adalah:
Pada soal diketahui titik P(-3, 5) maka:
Jadi bayangannya adalah P’(-5, 3)
Jawaban yang tepat A.
3. Jika titik B (5, -3) dicerminkan terhadap gari x = 2, koordinat titik bayangannya adalah...
a. (3, 1)
b. (-1, 3)
c. (-1, -3)
d. (3, -1)
Jawab:
Rumus pencerminan titik A(x, y) terhadap garis x = m adalah:
Pada soal diketahui titik B(5, -3) dan garis x = 2, maka:
Jadi bayangannya adalah B’(-1, -3)
Jawaban yang tepat C.
4. Koordinat titik bayangan dari R (4, -2) oleh dilatasi terhadap titik pusat O (0, 0) dengan faktor skala – ½ adalah...
a. (0, 1)
b. (-2, 1)
c. (-1, -2)
d. (2, 0)
Jawab:
Rumus bayangan dilatasi titik A(x, y) dengan pusat O dan faktor skala k adalah:
Pada soal diketahui titik R(4, -2) pusat O dan faktor skala – ½ maka:
Jadi bayangannya R’(-2, 1)
Jawaban yang tepat B.
5. Bayangan dari garis -2x + 5y = 10 yang ditranslasikan oleh T =  adalah...
adalah...
a. 2x + 4y = -20
b. 2x + y = -5
c. 2x + 2y = 10
d. 2x – 5y = -29
Jawab:
Rumus translasi titik A(x, y) oleh translasi T = (a¦b) adalah:
Pada soal diketahui garis -2x + 5y = 10 dengan translasi T = 
Maka:
Sehingga diperoleh:
x’ = x – 2 sehingga x = x’+ 2
y’ = y + 3 sehingga y = y’ - 3
-2x + 5y = 10
Subtitusikan x dengan x’+ 2 dan y dengan y’ - 3
-2x + 5y = 10
-2(x’ + 2) + 5(y’ - 3)= 10
-2x’ – 4 + 5y’ – 15 = 10
-2x’ + 5y’ – 19 = 10
-2x’ + 5y’ = 10 + 19
-2x’ + 5y’ = 29 atau 2x’ – 5y’ = -29 (kita sesuaikan dengan PG nya)
Jawaban yang tepat D.
6. Bayangan titik B (1, -3) yang diputar sejauh 900 searah putaran jarum jam terhadap titik O (0, 0) adalah...
a. (-3, -1)
b. (1, 3)
c. (3, 0)
d. (1, 0)
Jawab:
Rumus bayangan titik A(x, y) dengan rotasi [O, 900] (tanda – menandakan arah yang searah putaran jarum jam ) adalah:
Pada soal diketahui titik B(1, -3) maka:
Jadi, bayangannya adalah B’(-3, -1)
Jawaban yang tepat A.
7. Jika garis 3x – 2y = 6 ditranslasikan oleh T = , bayangan garis tersebut adalah...
, bayangan garis tersebut adalah...
a. 3x – 2y = 23
b. 3x - 2y = 15
c. 3x – 2y = -2
d. 3x – 2y = -11
Jawab:
Rumus translasi titik A(x, y) oleh translasi T = (a¦b) adalah:
Pada soal diketahui garis 3x – 2y = 6 dengan translasi T = 
Maka:
Sehingga diperoleh:
x’ = x + 3 sehingga x = x’- 3
y’ = y - 4 sehingga y = y’ + 4
3x – 2y = 6
Subtitusikan x dengan x’- 3 dan y dengan y’ + 4
3x – 2y = 6
3(x’ - 3) – 2(y’ + 4) = 6
3x’ – 9 – 2y’ – 8 = 6
3x’ – 2y’ – 17 = 6
3x’ – 2y’ = 6 + 17
3x’ – 2y’ = 23
Jawaban yang tepat A.
8. Perhatikan gambar berikut!
Bayangan titik P pada gambar di atas adalah...
a. (-11, 5)
b. (-12, 5)
c. (-13, 5)
d. (-14, 5)
Jawab:
Rumus pencerminan titik A(x, y) terhadap garis x = m adalah:
Pada soal diketahui titik P(5, 5) dan garis x = -3, maka:
Jadi bayangannya adalah P’(-11, 5)
Jawaban yang tepat A.
9. Bayangan titik A (7, -2) oleh dilatasi [O, 3] adalah..
a. (21, -6)
b. (10, -5)
c. (-5, 6)
d. (-3, 12)
Jawab:
Rumus bayangan dilatasi titik A(x, y) dengan pusat O dan faktor skala k adalah:
Pada soal diketahui titik A(7, -2) pusat O dan faktor skala 3 maka:
Jadi bayangannya R’(21, -6)
Jawaban yang tepat A.
10. Bayangan garis 3x – 2y + 6 = 0 oleh dilatasi [O, 2] adalah ...
a. x – y = 11
b. 3x + 2y = 5
c. 3x – 2y = -12
d. x – 3y = -10
Jawab:
Rumus bayangan dilatasi titik A(x, y) dengan pusat O dan faktor skala k adalah:
Pada soal diketahui titik A(x, y) pusat O dan faktor skala 2 maka:
Maka:
x’ = 2x sehingga x = ½ x’
y’ = 2y sehingga y = ½ y’
Subtitusikan x = ½ x’ dan y = ½ y’ pada persamaan:
3x – 2y + 6 = 0
3( ½ x’) – 2 ( ½ y’) + 6 = 0
3/2x’ – y’ + 6 = 0 (kalikan dengan 2) menjadi:
3x’ – 2y’ + 12 = 0 atau 3x’ – 2y’ = -12
Jawaban yang tepat C.
11. Garis x – 2y – 3 = 0 dicerminkan terhadap sumbu Y, maka persamaan bayangannya adalah...
a. x – 2y – 3 = 0
b. x + 2y – 3 = 0
c. –x – 2y – 3 = 0
d. –x + 2y + 3 = 0
Jawab:
Rumus pencerminan titik A(x, y) terhadap sumbu y adalah:
Maka diperoleh:
x’ = -x sehingga x = -x’
y’ = y sehingga y = y’
subtitusikan x = -x’ dan y = y’ pada persamaan:
x – 2y – 3 = 0
(-x’) – 2y’ – 3 = 0
-x’ – 2y’ – 3 = 0
Jawaban yang tepat C.
12. Bayangan titik A (-2, 7) oleh dilatasi [(-1, 3), 2] adalah...
a. (-8, 10)
b. (-3, 11)
c. (-4, 10)
d. (2, 5)
Jawab:
Rumus bayangan dilatasi titik A(x, y) dengan pusat M(a, b) dan faktor skala k adalah:
Pada soal diketahui titik A(-2, 7) pusat (-1, 3) dan faktor skala 2 maka:
= (-1 + 2(-1), 3 + 2(4))
= (-3, 11)
Jadi bayangannya A’(-3, 11).
Jawaban yang tepat B.
13. Jika pada dua buah segitiga siku-siku sisi miringnya sama panjang dan satu sudut lancipnya sama besar, sisi siku-siku yang bersesuaian akan...
a. Sama panjang
b. Tidak sama panjang
c. Mungkin sama dan mungkin beda
d. Tidak dapat ditentukan
Jawab:
Jawaban yang tepat adalah A. Pasti akan sama panjang juga.
14. Pada sebuah segitiga sama sisi terdapat tiga garis tinggi. Ketiga garis tinggi tersebut akan membagi segitiga menjadi...
a. Tiga segitiga yang kongruen
b. Empat segitiga yang kongruen
c. Lima segitiga yang kongruen
d. Enam segitiga yang kongruen
Jawab:
Perhatikan gambar berikut:
Pada gambar terlihat 6 pasang segitiga yang kongruen.
Jawaban yang tepat D.
15. Diketahui panjang pada ketiga sisi segitiga PQR berturut-turut 12 dm, 15 dm, dan 20 dm. Panjang sisi-sisi segitiga berikut yang sebangun dengan segitiga PQR adalah...
a. 12 dm, 9 dm, dan 15 dm
b. 10 dm, 8 dm, dan 12 dm
c. 25 dm, 16 dm, dan 9 dm
d. 75 dm, 60 dm, dan 100 dm
Jawab:
Syarat sebangun adalah sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Mari kita bahas satu persatu:
Pilihan A, 12/9 = 15/12 = 20/15 (salah)
Pilihan B, 12/8 = 15/10 = 20/12 (salah)
Pilihan C, 12/9 = 15/16 = 20/25 (salah)
Pilihan D, 12/60 = 15/75 = 20/100 benar yaitu bernilai 1/5
Jawaban yang tepat D.
16. Diketahui segitiga ABC dan DEF kongruen. Panjang sisi AC = 10 cm, panjang sisi BC = 15 cm dan <ACB = 650. Panjang sisi DF = 10 cm, panjang sisi DE = 13 cm, dan besar <EDF = 700. Besar <DEF adalah...
a. 450
b. 550
c. 650
d. 750
Jawab:
Perhatikan gambar berikut:
< A = < D = 700
< E = < B = 1800 – (700 + 650) = 1800 – 1350 = 450
Jawaban yang tepat A.
17. Perhatikan gambar di bawah ini!
Panjang BC pada gambar di atas adalah....
a. 24 cm
b. 18 cm
c. 12 cm
d. 9 cm
Jawab:
4 BC = 6 . 8
4 BC = 48
BC = 48 : 4
BC = 12
Jawaban yang tepat C.
18. Perhatikan gambar berikut!
Jika keduanya sebangun, panjang sisi PQ adalah..
a. 20 cm
b. 22 cm
c. 24 cm
d. 26 cm
Jawab:
12 PQ = 18 . 16
12 PQ = 288
PQ = 288 : 12
PQ = 24
Jawaban yang tepat C.
19. Dua bangun segitiga dikatakan kongruen apabila...
a. Sisi-sisi yang bersesuaian sama panjang
b. Sudut-sudut yang bersesuaian tidak sama besar
c. Salah satu sudut harus 900
d. Perbandingan sisi-sisinya tetap
Jawab:
Dua bangun dikatakan kongruen jika sisi-sisi yang bersesuaian sama panjang.
Jawaban yang tepat A.
20. Perhatikan segitiga berikut!
Jika segitiga ABC dan DEF kongruen, pernyataan berikut yang benar adalah...
a. Besar <B = <F dan panjang AB = EF
b. Besar <A = <D dan panjang AB = DE
c. Besar <C = <F dan panjang AC = EF
d. Besar <A = <E dan panjang BC = DE
Jawab:
Mari kita bahas satu-persatu pilihan di atas:
Pilihan A, salah, karena <B = < D
Pilihan B, salah, karena <A = <E
Pilihan C, benar
Jawaban yang tepat C.
21. Pada ∆ABC, AB = AC, CE tegak lurus AB, dan BD tegak lurus AC, yang merupakan pasangan segitiga sebangun adalah..
a. ∆BDC dengan ∆BEC
b. ∆AEC dengan ∆BEC
c. ∆AEC dengan ∆ABD
d. ∆ABD dengan ∆EBC
Jawab:
Berdasarkan gambar di atas mari kita bahas satu-persatu pilihan di atas:
Pilihan A, salah.
Pilihan B, benar.
Jawaban yang tepat B.
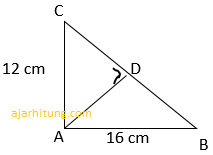
22. Perhatikan gambar berikut!
Panjang AD pada gambar di atas adalah...
a. 9,6 cm
b. 7,2 cm
c. 5,2 cm
d. 4,6 cm
Jawab:
Kita cari panjang BC menggunakan rumus pythagoras.
BC = √400
BC = 20
Selanjutnya kita cari luas segitiga:
L = 96 cm2
Untuk mencari panjang AD, kita gunakan rumus luas segitiga dengan alasnya BC.
96 = 10 AD
AD = 96 : 10
AD = 9,6
Jawaban yang tepat A.
23. Diketahui ∆ABC dan ∆PQR kongruen, besar <ABC = 800, <QRP = 500, dan panjang QR = 10 cm, maka besar <ACB adalah...
a. 500
b. 800
c. 1000
d. 1800
Jawab:
Perhatikan gambar berikut:
<ACB = 1800
– (800 + 500)
= 1800 – 1300
= 500
Jawaban yang tepat A.
24. Sebuah tiang tingginya 2 m memiliki bayangan 250 cm. Pada saat yang sama bayangan sebuah gedung 40 m. Tinggi gedung tersebut adalah...
a. 30 m
b. 32 m
c. 35 m
d. 50 m
Jawab:
Diketahui pada soal:
Tinggi tiang = 2 m
Bayangan tiang = 250 cm = 2,5 m
Bayangan gedung = 40 m
Tinggi gedung = x
2,5 x = 2 . 40
2,5 x = 80
x = 80 : 2,5
x = 32 m
Jadi tinggi gedung tersebut adalah 32 m
Jawaban yang tepat B.
25. Budi ingin mengukur tiang bendera yang ada di sekolahnya. Tinggi badan Budi adalah 170 cm. Budi berdiri di lapangan pada pagi hari menghadap tiang bendera yang ingin diukurnya. Panjang bayangan Budi 2,5 m dan bayangan tiang bendera 5 m. Tinggi tiang bendera tersebut adalah...
a. 3,6 m
b. 3,5 m
c. 3,4 m
d. 3,3 m
Jawab:
Pada soal diketahui:
Tinggi Budi = 170 cm = 1,7 m
Bayangan Budi = 2,5 m
Bayangan tiang = 5 m
Tinggi tiang = x
2,5 x = 1,7 . 5
2,5 x = 8,5
x = 8,5 : 2,5
x = 3,4
Jadi tinggi tiang bendera adalah 3,4 m
Jawaban yang tepat C.
Sampai disini ya adik-adik latihan kita. Kakak akan sambung 25 soal lagi di postingan setelah ini. Jadi, kalian jangan sampai ketinggalan. Kalian bisa langsung klik di link DISINI.





























No comments:
Post a Comment