Haloo adik-adik.. tidak terasa UAS semester ini segera datang.. ayo persiapkan diri kalian.... kakak akan menemani kalian mengingat materi selama 1 semester melalui latihan soal di bawah ini.
1. Nilai dari 32 – (-2) x 5 – 2 x (-3) adalah ...
a. 24
b. 32
c. 36
d. 48
Jawab:
32 – (-2) x 5 – 2 x (-3) = 32 – (-10) – (-6)
= 32 + 10 + 6
= 48
2. Pak Santosa membeli beberapa boks pensil. Setiap boks berisi setengah lusin pensil. Jika Pak Santosa membeli 25 boks dan tiap pensil harganya Rp800,-, maka harga pensil seluruhnya adalah...
a. Rp20.000,-
b. Rp100.000,-
c. Rp120.000,-
d. Rp200.000,-
Jawab:
1 lusin = 12 buah maka 1 boks berisi ½ x 12 buah = 6 buah.
25 boks x 6 pensil x Rp800,- = Rp120.000,-
Jadi, harga pensil seluruhnya adalah Rp120.000,-
3. Perbandingan buku Ayu : Dewi = 2 : 3 dan perbandingan buku Dewi : Linda = 4 : 7. Nlai perbandingan buku Ayu : Dewi : Linda adalah ...
a. 6 : 10 : 18
b. 8 : 12 : 21
c. 9 : 10 : 21
d. 9 : 12 : 24
Jawab:
(ikuti arah anak panah dan kalikan)
Ayu : Dewi : Linda = (2 x 4) : (4 x 3) : (3 x 7) = 8 : 12 : 21
Jadi, perbandingan buku Ayu : Dewi : Linda adalah 8 : 12 : 21 (B)
4. Dari sekelompok siswa, 35 orang gemar bermain bola basket, 23 orang gemar bermain bola voli, 9 orang gemar bermain kedua cabang olahraga tersebut dan 7 orang tidak menyukai keduanya. Jumlah siswa dalam kelompok tersebut adalah...
a. 49 orang
b. 56 orang
c. 60 orang
d. 64 orang
Jawab:
Yang suka basket dan voli = 9 orang
Yang suka basket saja = 35 – 9 = 26 orang
Yang suka voli saja = 23 – 9 = 14 orang
Yang tidak suka basket dan voli = 7 orang
Total siswa dalam kelompok = 9 + 26 + 14 + 7 = 56 orang
5. Enam buah buku harganya Rp15.000,-. Banyaknya buku yang dapat dibeli Umi jika ia membawa uang Rp20.000,- adalah...
a. 3 buku
b. 5 buku
c. 6 buku
d. 8 buku
Jawab:
Harga 1 buku = Rp15.000,- : 6 = Rp2.500,-
Buku yang didapat Umi = Rp20.000,- : Rp2.500,- = 8 buku
6. Diketahui P = {a,b,c,d,e}. Banyaknya himpunan bagian dari P yang mempunyai 3 anggota adalah..
a. 2
b. 7
c. 9
d. 10
Jawab:
P = {a,b,c,d,e}
Jumlah anggota P (n) = 5
Kita gunakan segitiga Pascal untuk mengerjakannya:
Perhatikan barisan angka yang menandakan himpunan beranggotakan 5. Barisannya adalah:
Pada soal ditanyakan himpunan bagian beranggotakan 3. Maka jumlahnya ada 10.
Jawaban yang tepat D.
7. Perhatikan gambar berikut!
Pecahan yang sesuai untuk daerah yang diarsir terhadap keseluruhan pada gambar adalah..
a. ¼
b. ¾
c. 3/8
d. 4/8
Jawab: bagian yang di arsir pada sebelah kiri jika digabungkan akan menjadi ¼ lingkaran. Jadi, lingkaran tersebut dibagi menjadi 4 bagian. Sedangkan yang diarsir adalah 2 bagian. Maka pecahan yang tepat adalah 2/4 = ½
Pada pilihan ganda, yang senilai dengan ½ adalah pilihan D 4/8 = ½.
Jadi, jawaban yang tepat adalah D.
8. Jika n(S) = 155, n(P) = 100, n(Q) = 120, dan n(P ∩ Q) = 80, maka nilai n(P ∪ Q)c adalah.....
a. 15
b. 35
c. 55
d. 140
Jawab:
Ingat rumus ini:
n(P ∪ Q) = n(P) + n(Q) – n(P ∩ Q)
pada soal diketahui:
n(S) = 155
n(P) = 100
n(Q) = 120
n(P ∩ Q) = 80
maka:
n(P ∪ Q) = n(P) + n(Q) – n(P ∩ Q)
= 100 + 120 – 80
= 140
(P ∪ Q)c artinya semua anggota semesta (S) yang bukan anggota (P ∪ Q)
(P ∪ Q)c = n(S) - n(P ∪ Q)
= 155 – 140
= 15
Jadi, jawaban yang tepat adalah A.
9. Diketahui jarak dua kota pada peta 25 cm. Jika skala yang digunakan oleh peta 1 : 250.000, maka jarak sebenarnya dari dua kota tersebut adalah...
a. 1.000 km
b. 100 km
c. 625 km
d. 62,5 km
Jawab:
Jarak peta = 25 cm
Skala = 1/250.000
Jarak sebenarnya = jarak peta : skala
= 25 cm : 1/250.000
= 25 cm x 250.000/1
= 6.250.000 cm
= 62,5 km
10. Dua belas orang bekerja selama 5 hari menghasilkan 900 rak buku. Jika 30 orang bekerja selama 6 hari, maka jumlah rak buku yang dihasilkan adalah...
a. 3.000 buah
b. 2.700 buah
c. 2.400 buah
d. 1.200 buah
Jawab:
1 orang dalam 1 hari mampu membuat = 900 rak : 12 orang : 5 hari
= 15 rak/ orang/ hari
30 orang dalam 6 hari mampu membuat = 30 orang x 6 hari x 15 rak/orang/hari
= 2.700 rak
11. Untuk menempuh jarak tertentu sebuah mobil melaju dengan kecepatan rata-rata 80km/jam, waktu yang diperlukan 3 jam 45 menit. Jika kecepatan rata-ratanya 60km/ jam, maka waktu yang diperlukan oleh mobil tersebut untuk menempuh jarak yang sama adalah...
a. 5 jam
b. 4 jam 40 menit
c. 4 jam 30 menit
d. 4 jam
Jawab:
Perbandingan di atas termasuk perbandingan berbalik nilai. Masih ingatkah kalian materi ini? Bagi kalian yang lupa, kalian bisa me recall materinya DISINI
60 x = 300
x = 300 : 60
x = 5
jadi, waktu yang diperlukan oleh mobil tersebut untuk menempuh jarak yang sama adalah 5 jam.
12. Sebuah proyek yang dikerjakan oleh 8 orang dapat selesai dalam waktu 15 hari. Supaya proyek tersebut selesai dalam waktu 12 hari, banyaknya pekerja yang perlu ditambahkan adalah ...
a. 2 orang
b. 3 orang
c. 4 orang
d. 10 orang
Jawab:
Soal di atas adalah perbandingan berbalik nilai, maka:
12 . x = 8 . 15
12x = 120
x = 120 : 12
x = 10
Maka, jumlah tambahan pekerjanya adalah = 10 orang – 8 orang = 2 orang
Jawab:
14. Perbandingan uang Budi dan Maria adalah 2 : 3, sementara itu perbandingan uang Budi dan Cici adalah 4 : 5. Jika jumlah uang mereka adalah Rp75.000,-, selisih uang Maria dan Cici adalah...
a. Rp5.000,-
b. Rp10.000,-
c Rp15.000,-
d. Rp20.000,-
Jawab:
Ikuti anak panahnya lalu kalikan angkanya:
Maria : Budi : Cici = (3 x 4) : (4 x 2) : (2 x 5)
Maria : Budi : Cici = 12 : 8 : 10
Selisih uang Maria dan Cici adalah =
= 2 x Rp2.500,-
= Rp5.000,-
15. Perhatikan gambar berikut!
Nilai pecahan yang ditunjukkan oleh daerah yang tidak diberi warna terhadap keseluruhan (segitiga kecil) pada gambar di atas adalah...
a. ½
b. 1/3
c. 2/6
d. 2/3
Jawab:
Segitiga yang tidak diarsir ada 6
Jumlah seluruh segitiga ada 9
Pecahannya = 6/9 = 2/3
16. Pak Salim memelihara ayam sebanyak 36 ekor. Persediaan pakan ayam yang ada di gudang diperkirakan cukup untuk 20 hari. Jika Pak Salim membeli ayam lagi sebanyak 4 ekor, maka persediaan pakan ayam di gudang akan cukup...
a. 18 hari
b. 19 hari
c. 23 hari
d. 24 hari
Jawab:
Perbandingan di atas termasuk perbandingan berbalik nilai.
40 . x = 36 . 20
40x = 720
x = 720 : 40
x = 18 hari
Jadi, persediaan pakan ayam di gudang akan cukup untuk 18 hari.
17. Di bawah sinar matahari, panjang bayangan sebuah pohon 12 m. Pada saat yang sama, panjang bayangan Roy yang tingginya 150 cm sama dengan 2m. Berarti tinggi pohon yang sebenarnya adalah...
a. 6 m
b. 8 m
c. 9 m
d. 16 m
Jawab:
Panjang bayangan pohon = 12 m
Panjang pohon = x m
Panjang bayangan Roy = 150 cm = 1,5 m
Panjang Roy = 2 m
1,5 . x = 12 . 2
1,5x = 24
x = 24 : 1,5
x = 16 m
Jadi, tinggi pohon yang sebenarnya adalah 16 m
18. Salah satu faktor dari x2 + 12x + 27 adalah...
a. 2x + 9
b. x – 9
c. x – 3
d. x + 9
Jawab:
Kakak akan kerjakan dengan cara pemfaktoran. Bagi kalian yang lupa materi ini, kalian bisa cek lagi DISINI.
Faktor-faktornya dapat dituliskan = (x + 3)(x + 9)
Jadi, salah satu akarnya adalah (x + 9)
19. Bentuk faktor dari x2 + y2 + m2 + n2 – 2xy + 2mn adalah...
a. (x – y)2 + (m – n)2
b. (x + y)2 + (m + n)2
c. (x – y)2 + (m + n)2
d. (x + y)2 + (m – n)2
Jawab:
x2 + y2 + m2 + n2 – 2xy + 2mn akan kakak kelompokkan menjadi:
x2 + y2 – 2xy + m2 + n2 + 2mnbentuk ini adalah hasil kuadrat dari: (x – y)2 + (m + n)2
jadi, jawaban yang tepat adalah C
a. 25m
b. 8m
c. 8/m
d. m/8
jawab:
21. Bentuk sederhana dari  adalah...
adalah...
Jawab:
22. Bentuk sederhana dari  adalah ...
adalah ...
Jawab:
Jadi, jawaban yang tepat adalah C.
23. Diketahui bentuk aljabar 6x5 – 3x4 + 12x3 – x2 + 5x + 8. Koefisien dari x3, x2, dan x berturut-turut adalah...
a. 6, -3, dan 12
b. 12, 1, dan 5
c. 12, -1, dan 5
d. 12, 5, dan 8
Jawab:
Koefisien dari x3 = 12
Koefisien dari x2 = -1
Koefisien dari x = 5
24. Hasil dari 12a2b3 : 4ab adalah...
a. 3a3b2
b. 3ab2
c. 3a2b
d. 3a2b2
Jawab:
12a2b3 : 4ab = (12 : 4) (a2-1) (b3-1)
= 3a1b2
= 3ab2
25. Hasil penjabaran dari  adalah...
adalah...
Jawab:
Jadi, jawaban yang tepat adalah B.
26. Pernyataan di bawah ini yang bukan merupakan persamaan linear satu variabel adalah...
a. a + 2 = 6
b. y + 8 = 4y – 6
c. x – 21 = 8x
d. 3x – y = 10
Jawab:
Mari kita bahas satu-satu pilihan ganda di atas:
Pilihan A satu variabel, yaitu a
Pilihan B satu variabel, yaitu y
Pilihan C satu variabel, yaitu x
Pilihan D dua variabel, yaitu x dan y
Jadi, pilihan yang tepat adalah D.
27. Persamaan 3(2x – 1) – (5x – 8) = 17 ekuivalen dengan persamaan...
a. 2x + 1 = 0
b. x– 2 = 10
c. 2x – 2 = 10
d. 3x – 1 = 10
Jawab:
Ekuivalen artinya memiliki nilai x yang sama nilainya.
3(2x – 1) – (5x – 8) = 17
6x – 3 – 5x + 8 = 17
6x – 5x – 3 + 8 = 17
x + 5 = 17
x = 17 – 5
x = 12
Selanjutnya, dari opsi ABC dan D di atas, cari yang nilai x = 12. Mari kita bahas satu persatu:
Pilihan A, 2x + 1 = 0
2x = -1
x = -1/2
Pilihan B, x – 2 = 10
x = 10 + 2
x = 12
Jadi, jawaban yang tepat adalah B.
28. Penyelesaian dari  adalah ...
adalah ...
a. -4
b. 4
c. ¼
d. – ¼
Jawab:
29. Penyelesaian dari x – 6 > 15 adalah...
a. x > 21
b. x > -9
c. x > 9
d. x > -21
Jawab:
x – 6 > 15
x – 6 + 6 > 15 + 6
x > 21
30. Sebuah persegi panjang mempunyai ukuran panjang (3x – 2) cm dan lebar (x + 4) cm. Jika keliling persegi panjang 44 cm, maka panjang dan lebar persegi panjang tersebut berturut-turut adalah..
a. 15 cm dan 7 cm
b. 14 cm dan 8 cm
c. 13 cm dan 9 cm
d. 12 cm dan 10 cm
Jawab:
Panjang = (3x – 2)cm
Lebar = (x + 4)cm
Keliling persegi panjang = 2 (panjang + lebar)
44 = 2 ((3x – 2)+ (x + 4)
44 = 2(4x + 2)
44 = 8x + 4
8x = 44 – 4
8x = 40
x = 40 : 8
x = 5
Panjang = (3x – 2)cm = 3(5) – 2 = 15 – 2 = 13 cm
Lebar = (x + 4)cm = 5 + 4 = 9 cm
Selamat menyiapkan diri untuk UAS semester I ya adik-adik. Kakak doakan kalian mendapatkan nilai seperti yang kalian harapkan.. semangat...






















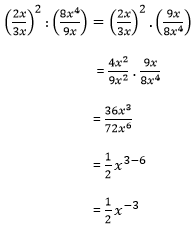



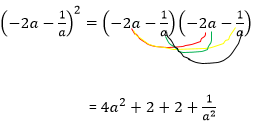


No comments:
Post a Comment